Los principales en el Teorema de álgebra lineal y el Teorema de geometría algebraica. Estos derivan a muchos otros teoremas que serán mencionados a continuación:
01. Teorema de Ruffini: 

02. Teorema fundamental del álgebra (p.ejemplo: x-1=3)
03. Teorema de Artin-Wedderburn
04. Teorema del Binomio:
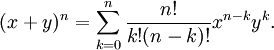
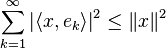
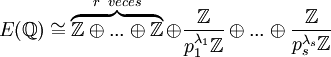
Son teoremas que ayudan y/o solucionan cualquier tipo de ecuación o problema que se no presente. Tienen nombres de grandes filósofos ya que fueron ellos mismos los que los crearon y aplicaron en la antigüedad.
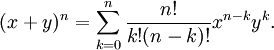
05. Teorema de Cauchy (agrupación):
" para todo grupo finito G, sí existe un primo p tal que p|o(G), (p divide al orden del grupo g, donde el orden del grupo es el número de elementos de G), entonces existe H ≤ G (H subgrupo de G) tal que o(H) = p, (el orden de H es p, donde p es el número de elementos de H)"
" para todo grupo finito G, sí existe un primo p tal que p|o(G), (p divide al orden del grupo g, donde el orden del grupo es el número de elementos de G), entonces existe H ≤ G (H subgrupo de G) tal que o(H) = p, (el orden de H es p, donde p es el número de elementos de H)"
06. Teorema de los ceros de Hilbert: I(V(J)) = √J para todo ideal J
07. Desigualdad de Bessel:
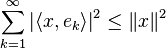
08. Teorema del factor
09. Teorema de Frobenius
10. Teorema de Galois
11. Teorema de homomorfismos:
12. Identidad de Brahmagupta:
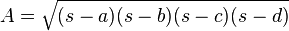
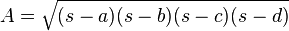
13. Teorema de Isomorfia:
14. Teorema de Kronecker Weber
15. Teorema de Lagrange
16. Teorema de Lindemann
17. Teorema de Maschke:
18. Teorema de Mordell:
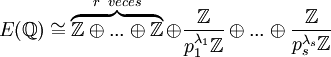
19. Teorema del resto: dividir un polinomio 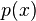 entre
entre  , es igual a
, es igual a 
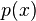 entre
entre  , es igual a
, es igual a 
20. Teorema de Skolem: g(a) = b·f(a)b-1
Son teoremas que ayudan y/o solucionan cualquier tipo de ecuación o problema que se no presente. Tienen nombres de grandes filósofos ya que fueron ellos mismos los que los crearon y aplicaron en la antigüedad.

